Floor Function Properties

And this is the ceiling function.

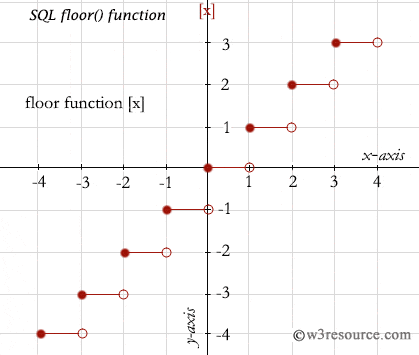
Floor function properties. Definition properties and wonderful examples. For example the floor and ceiling of a decimal 3 31 are 3 and 4 respectively. The article makes a brief summary on the frequently used properties of the floor function. So with the help of these two functions we get the nearest integer in a number line of a given decimal.

Definite integrals and sums involving the floor function are quite common in problems and applications. The properties include basic inequalities conditional inequalities and basic equalities that are. A useful way to use the floor function is to write where y is an integer and k is the leftover stuff after the decimal point. Unfortunately in many older and current works e g honsberger 1976 p.

Aslo the ceiling function of course but just. In this article let us discuss the ceiling function definition notation properties graphs. R r must be continuous and monotonically increasing and whenever f x f x f x is integer we must have that x x x is integer. Int limits 0 infty lfloor x rfloor e x dx.

In mathematics and computer science the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to denoted or similarly the ceiling function maps to the least integer greater than or equal to denoted or. Koether hampden sydney college direct proof floor and ceiling wed feb 13 2013 3 21. For example and while. Examples for example b3 8c 3.

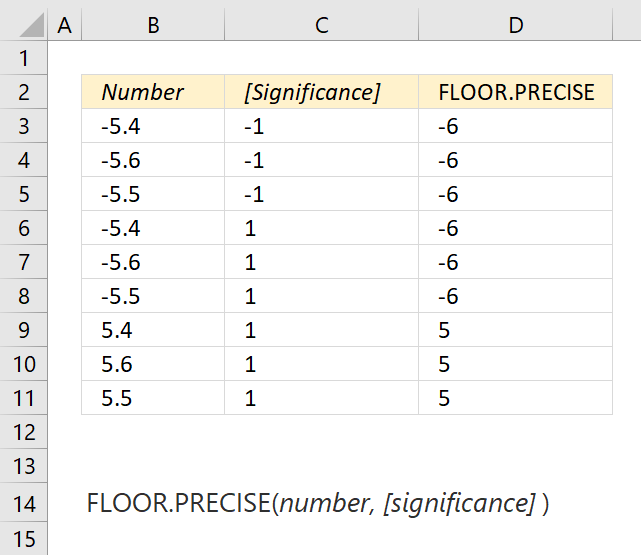
This can greatly simplify many problems. The int function short for integer is like the floor function but some calculators and computer programs show different results when given negative numbers. Mathbb r rightarrow mathbb r f. Iverson graham et al.

The floor function also called the greatest integer function or integer value spanier and oldham 1987 gives the largest integer less than or equal to the name and symbol for the floor function were coined by k. Definition the floor function let x 2r. Such a function f. 0 x.

Definition the ceiling function let x 2r. Define bxcto be the integer n such that n x n 1. The best strategy is to break up the interval of integration or summation into pieces on which the floor function is constant. R r f.

Certain functions have special properties when used together with floor and ceil. For all real. Evaluate 0 x e x d x. Define dxeto be the integer n such that n 1 x n.